Static value vs monthly additions - Compounded over 25 years
Oct 13, 2020VTS Community,
There was a lot of great feedback from yesterdays blog so we'll keep it going with a follow up while it's still fresh in our minds. If you missed it, you can check it out here:
Article: The importance of adding money to an investment account
I showed the incredible compounding effect of making regular contributions to an investment account. Just to refresh the memory, here's the comparison of adding 1,000$ a month to the VTS Total Portfolio Solution since it launched in January 2012, vs making no additional contributions.
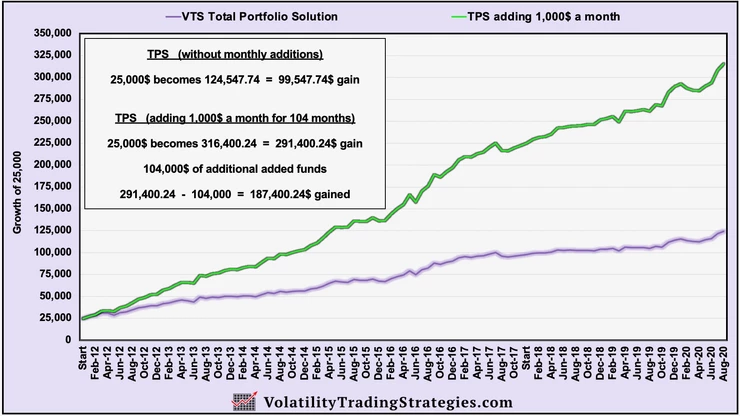
After backing out all contributions, the person making regular additions would have nearly twice as much profit. That's the power of compounding!
Now this is something that we all intuitively know right? If we save money and add it to the lump sum every month, of course we'll have more money long term, it's obvious. However, until people actually see it on a chart, sometimes it just doesn't register quite how dramatic the long term effect can be. I had some great follow up questions which I'll get into today:
1) What does it look like over 25 years?
2) What if instead of 1,000$ I can only contribute 300$ a month?
3) What if I can save as much as 3,000$ a month?
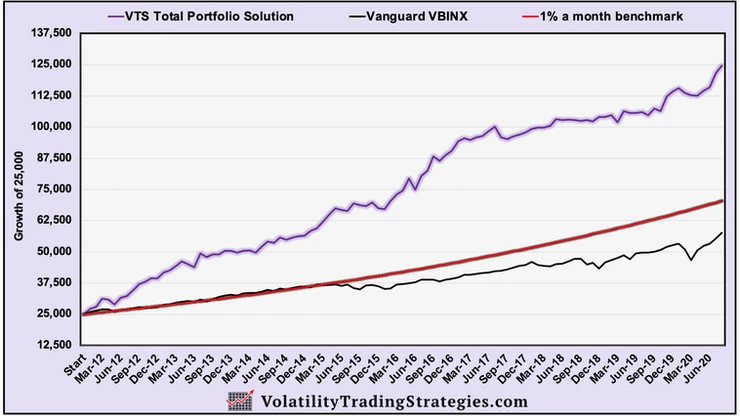
So the first thing we need is a realistic rate of return over the next 25 years to work with. Now the VTS Total Portfolio Solution will be 9 years old at the end of 2020, and it has returned 20% a year since inception. In every 5-10 year period we will naturally have some great years that will make that kind of return possible.
So while I do think it's realistic (and my goal) to get a solid double digit return indefinitely, when running hypotheticals it is wise to use a more conservative number. The official benchmark we measure our results against is the Vanguard VBINX, a 60/40 balanced index fund. We crush that and I think that will be even more true with each market crash going forward.
But my own personal long-term benchmark is 1% a month.
It's my goal to keep my performance above a hypothetical 1% a month for my entire investing career. If I do that, I know I'll be happy with my own account value, and I don't think anybody else would complain either :)
So for today's 25 year simulation, let's use 1% a month as the official return.
1% a month for 25 years: No additions vs adding 1,000$ / mo
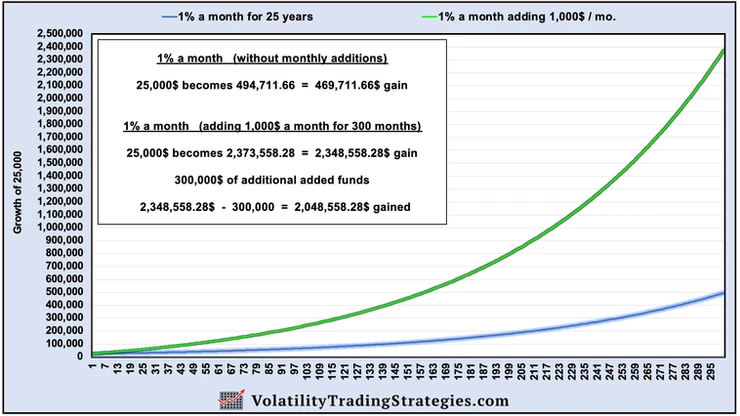
For all of these comparisons, we always back out the full amount of starting capital plus all the additional capital added along the way. So in this example, we will subtract the 25,000$ start value, plus we'll also subtract the 300,000$ that was added over the 25 years.
No additions net profit: 469,711.66$
Adding 1,000$ / mo net profit: 2,048,558.28$
The investor who lived below their means and added 1,000$ a month to their trading account would have over 4 times the net profit, and would build up a nice 2+ million retirement fund.
Now of course I'm fully aware of all the income and savings rate statistics in developed countries, so I'm not blind to the fact that adding 1,000$ a month may be a stretch for some people depending on their situation.
If you can't, set that as a longer term goal. You could even consider starting a little "side hustle" on the weekends and maybe build up a 500$ or 1,000$ a month online income. In 2020, that's possible for everyone.
But remember, every little bit helps! Can you add 300$ / month?
1% a month for 25 years: No additions vs adding 300$ / mo
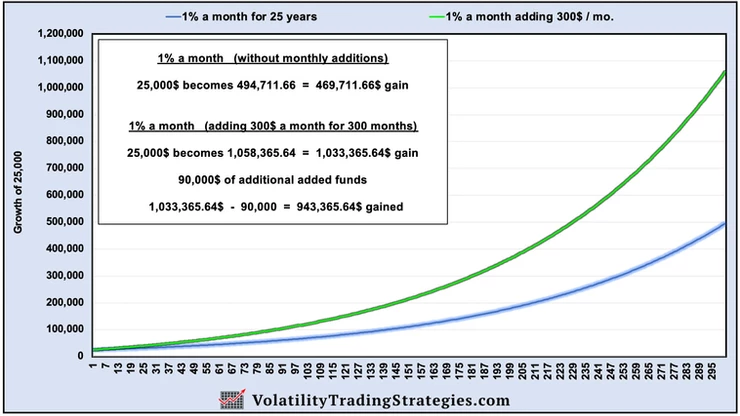
Backing out the original 25,000$ and the 90,000$ that the 2nd investor has added over the years.
No additions net profit: 469,711.66$
Adding 300$ / mo net profit: 943,365.64$
Even by adding just 300$ a month, the investor would potentially double their net profit in the long run and still reach a million dollar retirement fund 25 years later. The idea that you have to have a large income to retire a millionaire is simply not true. Now granted, it helps, obviously. But remember, retiring a millionaire isn't as out of reach as many people believe:

People always assume that multimillionaires, the "1%" must make huge incomes that are totally unreasonable for the average person to achieve. But is it possible that they just follow the 3 steps from above?
What if they aren't a high powered lawyer or doctor? What if they just make a solid income, live below their means, and manage to save 3,000$ a month?
1% a month for 25 years: No additions vs adding 3,000$ / mo
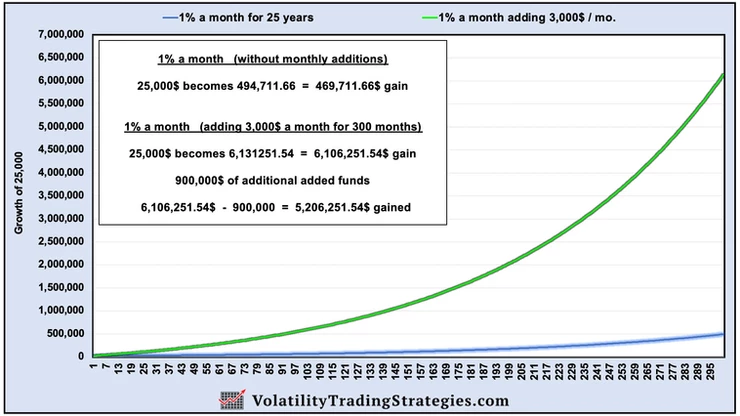
Backing out the 25,000$ plus the 900,000$ that this person added:
No additions net profit: 469,711.66$
Adding 3,000$ / mo net profit: 5,206,251.54$
Nothing would make me happier than if each and every one of you in the VTS community was able to build up a multi-million dollar retirement fund. When you do, your friends will naturally assume that you had some insane income in your life.
You'll answer: "Not really. I just lived below my means, saved a few thousand dollars a month, and followed tactical investment strategies that avoided major drawdowns and made me a double digit return long term. It was just the power of compounding and a little help from father time."
Take Control of your Financial Future!
Profitable strategies, professional risk management, and a fantastic community atmosphere of traders from around the world.

